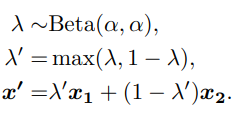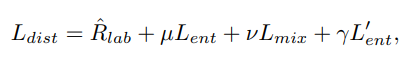2022-CVPR-[Dist-PU] Positive-Unlabeled Learning from a Label Distribution Perspective

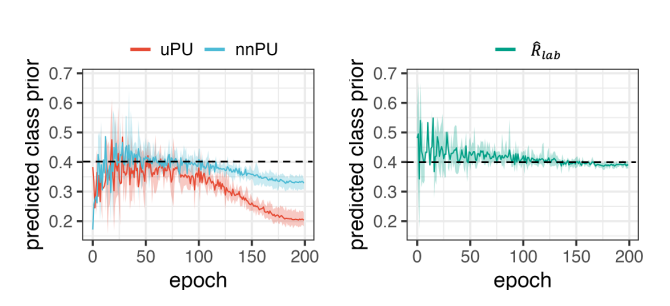
PUのCost-sensitiveの研究は、Negative Assumptionといって過度にデータをNegativeに分類させてしまう。以下のように、全体の割合の0.4から大きく逸脱することになる。

なので、U Dataについての予測した各サンプルのスコアの平均とClass Priorが大きく逸れないようにしたい。だが、明示的な解としてすべてのUの予測が $\pi$ になってしまうのがあるので、それを防ぐためにEntropyの項をつけた。

$\mathbf{x} \in X \subseteq \mathbb{R}^d$ で、Ground Truthのラベル $y=1$ はPで $y=0$ がN。
2setのいずれでも問題はない。

Cost-sensitiveの式で導いた時、

この2点がこの手法の提案の核心。

nnPUの式は以下のようになる。

\pi \mathbb{E}_+[l(g(\mathbf{x}), +1)] + |-\pi \mathbb{E}_+[l(g(\mathbf{x}), -1)] + \mathbb{E}_X[l(g(\mathbf{x}), -1)]|

だが、今回は以下のようなclippingをする。

2\pi \mathbb{E}_+[l(g(\mathbf{x}), +1)] + | \mathbb{E}_X[l(g(\mathbf{x}), -1)] - \pi|

実際は $g(\mathbf{x})$ の出力値をlogitとして扱いsigmoid関数 $f$ をかませて、 $f(g(\mathbf{x}))$ がクラスの予測確率である。そして、予測したラベルは本来離散的であるべきだが、これからの計算の都合上連続的であるようにする。

具体的には、あるデータ群に対するラベルの平均は、 $f(g(\mathbf{x}))$ の予測値の平均をとる感じである。この平均について、P全体では1に、U全体では $\pi$ になるようにしたい。

これは、以上のclippingされた式に対して、次のように目的の値からのズレで評価し、MAE損失を使う。

2\pi \mathbb{E}_+[l(g(\mathbf{x}), +1)] + | \mathbb{E}_X[l(g(\mathbf{x}), -1)] - \pi| \rightarrow \\ R_{lab} = 2\pi |\mathbb{E}_+[f(g(\mathbf{x}))] - 1| + | \mathbb{E}_X[l(g(\mathbf{x}), -1)] - \pi|

だが、このままではすべてのUの予測が $\pi$ に収束するような自明な解に収束してしまう。これを防ぐために、以下のような選択をする。

Ｕがすべて $\pi$ にならなくするには、Entropy Minimizationをさせて、全体的に極端な予測を行わせるようにする。Uのすべてのデータについて行う。

s = f(g(\mathbf{x}))\\ L_{ent} = - \mathbb{E}_X[(1 - s) \log (1 - s) + s \log s]

Entropy Minimizationは明確に分けるという目的を達成できるが、一方本来曖昧なものを極端に推し進めてしまうのもある。最初に間違えた予測のまま拡大されたら、まずい。

これはConfirmation Biasという。

これを解決するため、データを以下のようにMixupする。

そして、このようにMix-upしたデータに対して、以下のようにBinary Cross Entropyで損失を追加で計算する。

s^\prime = f(g(\lambda^\prime \mathbf{x}_1 + (1 - \lambda^\prime) \mathbf{x}_2))\\ L_{mix} = \mathbb{E}_{(\mathbf{x}_1, \mathbf{x}_2)} [\lambda^\prime l_{bce}(s^\prime, s_1) + (1 - \lambda^\prime) l_{bce}(s^\prime, s_2)]

これによって、曖昧なものを極端に推し進めづらくすることができる。

最後に、Mixupされたデータについても、Entropy Minimizationも行う。

ということで、全体では以下のようになる。

実際の実装では、

単純の「本体」と「本体のEntropy Minimization」だけでWarm Up。
1. lr=5e-4, 60epochs 走らせる。
「ミニバッチ内のMixup」と「ミニバッチ内のMixupされたデータのEntropy Minimization」を訓練に使う。(与えられたデータを純粋にそのまま学習に使うことはもうない)

ハイパーパラメタについては以下のように使っていた。 $\alpha$ はmixupのパラメタ。

\mu \in [0, 0.1] , \nu \in [0, 10], \gamma \in [0, 0.3], \alpha \in [0.1, 10]

スケジューラはcosineスケジューラを使った。